Threshold Signature Scheme ("TSS")
Swingby Skybridge is powered by the latest innovations in modern cryptography.
The Threshold Signature Scheme (TSS) is a cryptographic protocol where private keys (and cryptocurrency addresses being derived) can be created and shared by multiple parties.
A threshold number (i.e., a subset) of those parties can then follow the protocol to collaboratively produce valid signatures to sign cryptocurrency transactions without the parties needing to share any secret with each other. No trusted dealer is needed and the protocol is fully decentralized.
The Threshold Signature Scheme (TSS) coordinates between multiple parties to create digital signatures for cryptocurrency transactions. A single signature is produced for each one, which differs from multi-sig (and similar) script implementations in Bitcoin that require several independent digital signatures. Besides, this also means that a single signature mechanism can be used on any ECDSA signature chain, irrespective of whether the chain has natively multi-signature capabilities.
An additional benefit of TSS transactions over multi-signature transactions is their data lightness: they contain no more signature data than normal transactions and thus, are cheaper to verify. Any transaction fees (also known as mining fees, transaction fees, or gas) needed to compensate miners to process these transactions are kept to a minimum as there is only one signature accompanying the transaction.
Keygen phase
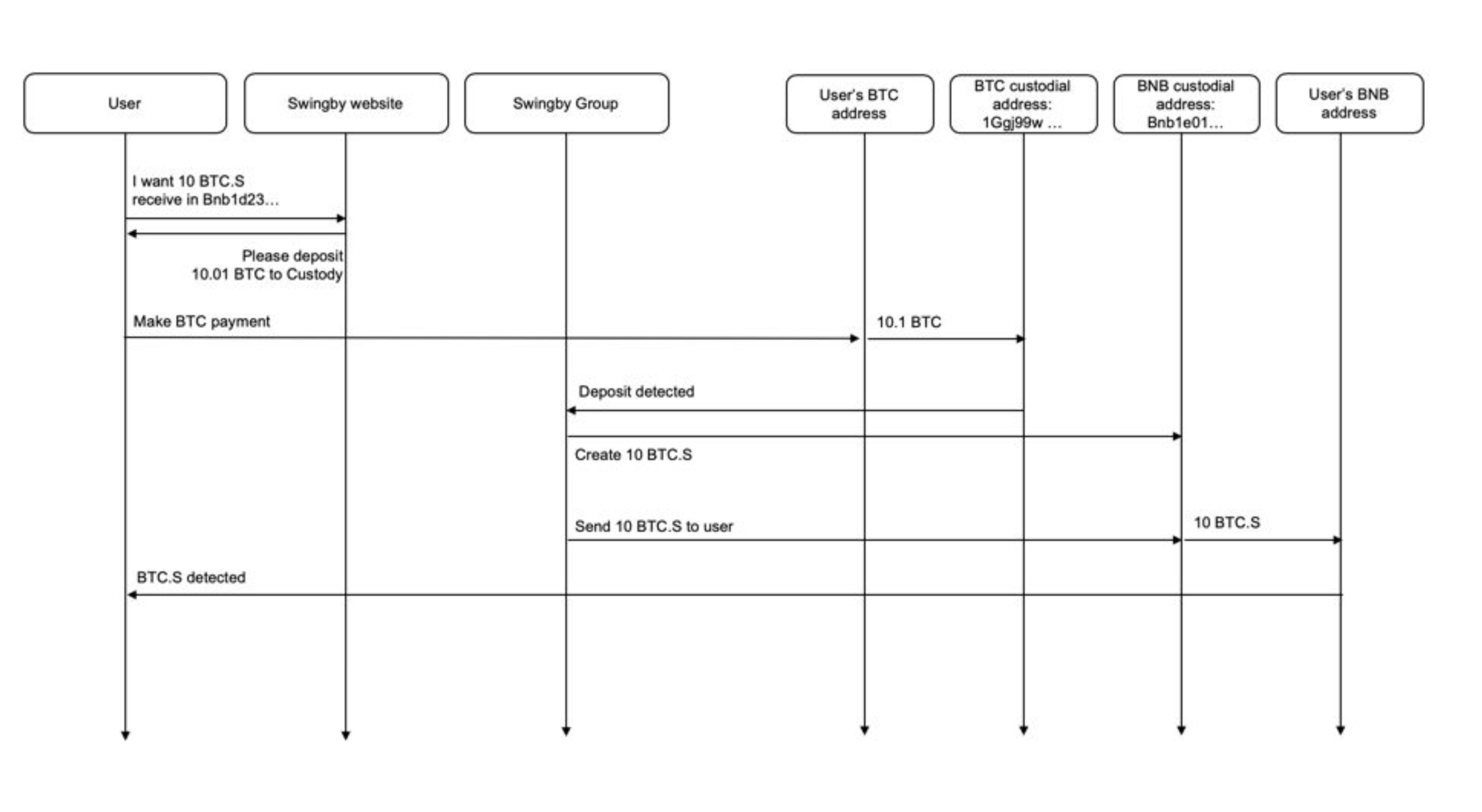
The TSS protocol is used to create, effectively, a single private key that is never known to any party or combination of parties. The public key related to that private key is known to all parties. That public key is then used to create an address on the source chain and on the destination chain, forming the bridge.
In the case of our first implementation, custodial addresses would be derived for both Bitcoin and Ethereum networks.
In the keygen phase, from the full set of nodes running on the Swingby Skybridge network, a subset is deterministically chosen and is known as the TSS group. The group selection is based on:
Consensus about the TSS parameters n and t (n = total number of nodes in the group, t = the threshold number of nodes who need to collaborate to generate a valid signature), and other settings such as fee rates.
Agreement on which chains the nodes are operating on, and whether they are using the test-nets.
The length of time the nodes have staked the minimum amount of SWINGBY.
For example, at one point in time the Swingby Network may consist of 150 nodes, of which 140 want to create a (n=100, t=60) token bridge. (Perhaps the other 10 nodes want to make a (n=8, t=5) token bridge).
The 140 eligible nodes are then ordered by the length of time they have staked their SWINGBY tokens (assuming they have all staked at least the minimum amount), and the top 100 nodes from that ordered list will form the TSS group for the keygen phase. This process explains how a TSS group is deterministically selected.
Transaction signing
When a new transaction needs to be created and signed by the TSS group, the process is as follows:
Each Swingby node independently builds up a list of peers that they are aware of on the Swingby network.
Each Swingby node independently advertises to other nodes on that list the message that they would like the TSS group to sign. This is called the “Sign List Building” round.
Each Swingby node independently but deterministically creates a set of (t) signers meeting the criteria. This is called the “Sign List Voting” round.
Each Swingby node independently runs the TSS rounds in parallel, and each one collects “signature shares” from other peers. At this stage there is a lot of communication and cross-checking.
Using the signature shares, each Swingby node can independently create the full ECDSA signature for the message.
Any of the Swingby nodes can broadcast the signed transaction to the relevant blockchain (Bitcoin or Binance Chain). This means that the blockchain will receive multiple similar transactions, all of which are identical - and only one of which will get through.
Last updated